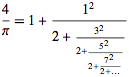Basic ideas and concepts:
- Why we assume that
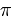 exists? In other words, why it is certain that the ratio of the circumference to its diameter is always the same for any given circle? Short answer: all circles are geometrically similar, and therefore the ratios of corresponding parts are proportional. For two circles, C1 and C2, of radii r1 and r2 must be true that: C1/r1 = C2/r2 which is equivalent to C1/d1 = C2/d2
exists? In other words, why it is certain that the ratio of the circumference to its diameter is always the same for any given circle? Short answer: all circles are geometrically similar, and therefore the ratios of corresponding parts are proportional. For two circles, C1 and C2, of radii r1 and r2 must be true that: C1/r1 = C2/r2 which is equivalent to C1/d1 = C2/d2
Long answer: Inscribe a regular hexagon in a circle. All angles of the hexagon are equal (60), all sides also equal, therefore, the perimeter of the hexagon of radius 1 is 6 and the ratio of the perimeter to the diameter (2r) is 3. Since equal chords cut off equal arcs, the perimeter of the circle will always keep the same ratio to its radius no matter the size of the circle.
- Why the letter
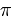 ? The letter
? The letter 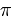 stands for perimeter, the distance around a figure. The ratio perimeter/diameter was written –in Greek letters— p/d. In 1706 the Welsh Mathematician William Jones dropped the d and started using the symbol
stands for perimeter, the distance around a figure. The ratio perimeter/diameter was written –in Greek letters— p/d. In 1706 the Welsh Mathematician William Jones dropped the d and started using the symbol 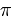 alone.
alone.
The symbol began to be extensively used after Leonhard Euler adopted it in 1737.
- A constant called
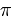 ? Since ancient times was observed that the ratio of the circumference of a plane circle to its diameter –the larger distance across-- was constant. This is, no matter how big or small the circle is that constant has a value of approximately 3.
? Since ancient times was observed that the ratio of the circumference of a plane circle to its diameter –the larger distance across-- was constant. This is, no matter how big or small the circle is that constant has a value of approximately 3.
- Which is the exact value of
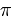 ? Most people respond to the value of pi as 3.14;
? Most people respond to the value of pi as 3.14; 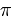 is a number whose decimal expansion neither ends nor repeats a block of digits, like rational numbers do. (Rational numbers can be expressed as ratio of integers).
is a number whose decimal expansion neither ends nor repeats a block of digits, like rational numbers do. (Rational numbers can be expressed as ratio of integers). 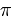 is considered an irrational number, one that cannot be expressed as a ratio of two integers. Today billions of digits of the expansion of pi have been calculated. These are the first fifty:
is considered an irrational number, one that cannot be expressed as a ratio of two integers. Today billions of digits of the expansion of pi have been calculated. These are the first fifty:
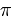 = 3.14159265358979323846264338327950... up to infinity.
= 3.14159265358979323846264338327950... up to infinity.
- How can a number be called irrational? Indeed “irrational” in this context should not be understood as “beyond reason”. Ancient Greeks called “logos” a ratio of two integers. Logos in Greeks also means word, verb, expressible. Numbers that were demonstrated not to be expressible as the ratio of two integers, like the square root of two, were called “alogos”, meaning “inexpressible”. Again, the decimal expansion of
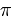 , like all irrational numbers, neither terminates nor become periodic.
, like all irrational numbers, neither terminates nor become periodic.
- Who proved the irrationality of
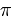 ? Johann H. Lambert in 1761. His approach goes as follows: He demonstrated that if x is a rational number, tangent of x is irrational; on the other hand, whenever tan(x) is rational, x must be irrational. Since tan(
? Johann H. Lambert in 1761. His approach goes as follows: He demonstrated that if x is a rational number, tangent of x is irrational; on the other hand, whenever tan(x) is rational, x must be irrational. Since tan(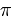 /4) = 1, therefore
/4) = 1, therefore 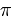 is irrational. There are other more convincing proofs of the irrationality of
is irrational. There are other more convincing proofs of the irrationality of 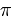 , this one was the first and simple enough to be understood by everyone.
, this one was the first and simple enough to be understood by everyone.
- Is
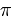 a transcendental number or an algebraic number? 1873 Charles Hermite proved that the euler’s number e, is transcendental. This is, there is no equation of the form aex + bey + cez +....= 0 where the coefficients a, b, c and the exponents x, y, z are rational numbers. Then in 1882, Ferdinand von Lindermann proved that
a transcendental number or an algebraic number? 1873 Charles Hermite proved that the euler’s number e, is transcendental. This is, there is no equation of the form aex + bey + cez +....= 0 where the coefficients a, b, c and the exponents x, y, z are rational numbers. Then in 1882, Ferdinand von Lindermann proved that 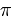 is transcendental based in Hermite’s work. Lindermann proved that the exponent in the “e’ equation cannot be either algebraic numbers, therefore eix + 1 = 0 is not satisfied when x is an algebraic number, therefore x must be transcendental. (The imaginary unit i is algebraic since √-1 = i).
is transcendental based in Hermite’s work. Lindermann proved that the exponent in the “e’ equation cannot be either algebraic numbers, therefore eix + 1 = 0 is not satisfied when x is an algebraic number, therefore x must be transcendental. (The imaginary unit i is algebraic since √-1 = i).
Note: For more info on this topic of the transcendentally of numbers, search on Lindemann–Weierstrass theorem .
- Squaring the circle. Is this possible? Since
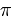 is transcendental, it is impossible to construct a square of equal area of a given circle. This is, it is impossible to construct a square of side √
is transcendental, it is impossible to construct a square of equal area of a given circle. This is, it is impossible to construct a square of side √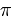 by using straightedge and compass and the ancient Greek attempted unsuccessfully.
In common language, the expression squaring the circle is used as a figure of speech for trying something obviously impossible.
by using straightedge and compass and the ancient Greek attempted unsuccessfully.
In common language, the expression squaring the circle is used as a figure of speech for trying something obviously impossible.
-
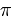 formulas: Nothing better that mathworld website as a reference for pi formulas:
formulas: Nothing better that mathworld website as a reference for pi formulas:
Pi Formulas
- Ramanujan, 1914:
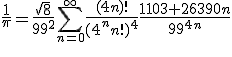
- Continued fractions of
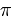 at Mathworld:
at Mathworld: